big O
For a given complexity function f(n), O(f(n)) is the set of complexity functions g(n) for which there exists some positive real constant c and some nonnegative integer N such that for all n ≥ N, g(n) ≤ c $\times$ f(n).
주어진 복잡도 함수 f(n)에 대해서 g(n) ∈ O(f(n))이면, n ≥ N인 모든 정수 n에 대해서 g(n) ≤ c $\times$ f(n)이 성립하는 실수 c > 0와 음이 아닌 정수 N이 존재한다.
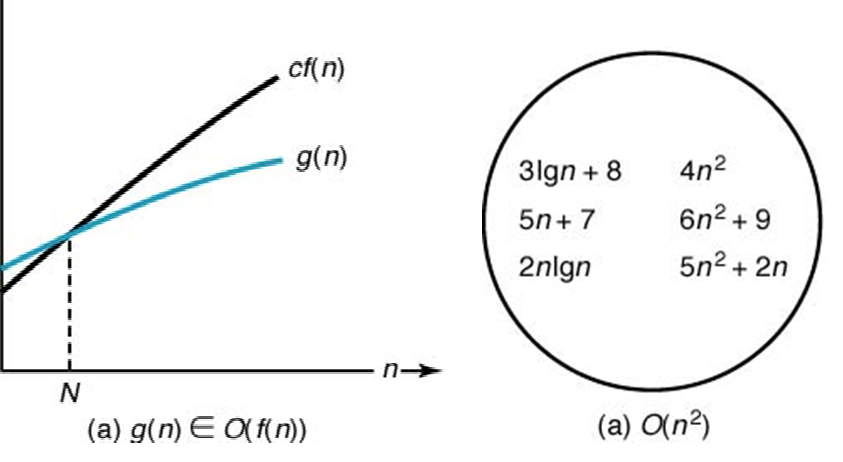
If g(n) ∈ O(f(n)), we say that g(n) is big O of f(n)
어떤함수 g(n)이 $O(n^2)$에 속한다는 말은, 그 함수는 궁극적으로 (어떤 임의의 N보다 큰 값에 대해서는) 어떤 2차함수 $c \times n^2$ 보다는 작은 값을 가지게 된다는 것을 뜻한다. 따라서 g(n)은 어떤 2차함수 $c \times n^2$보다는 궁극적으로 좋다고 말할 수 있다.
g(n) ∈ O(f(n))
- g(n): 분석된 결과
- O(f(n)): 기껏해야 f(n)의 비율로 증가하는 함수
- g는 f보다 빠르게 증가하지 않는다. (상수 비율의 차이는 무시)
an asymptotic upper bound: 점근적 상한
big O는 x가 증가할수록 g(x)보다 항상 스케일이 큰 f(x)를 찾는 것이다.
어떤 알고리즘의 시간복잡도가 O(f(n))이라면, 입력크기 n에 대해서 이 알고리즘의 수행시간은 아무리 늦어도 f(n)은 된다. 다시 말하면 이 알고리즘의 수행시간은 f(n)보다 절대로 더 느릴수는 없다는 말이다. (f(n)이 상한)
Omega
For a given complexity function f(n), Ω(f(n)) is the set of complexity functions g(n) for which there exists some positive real constant c and some nonnegative integer N such that, for all n ≥ N, g(n) ≥ c $\times$ f(n).
주어진 복잡도 함수 f(n)에 대해서 g(n) ∈ Ω(f(n))이면, n ≥ N인 모든 정수 n에 대해서 g(n) ≥ c $\times$ f(n)이 성립하는 실수 c > 0와 음이 아닌 정수 N이 존재한다.
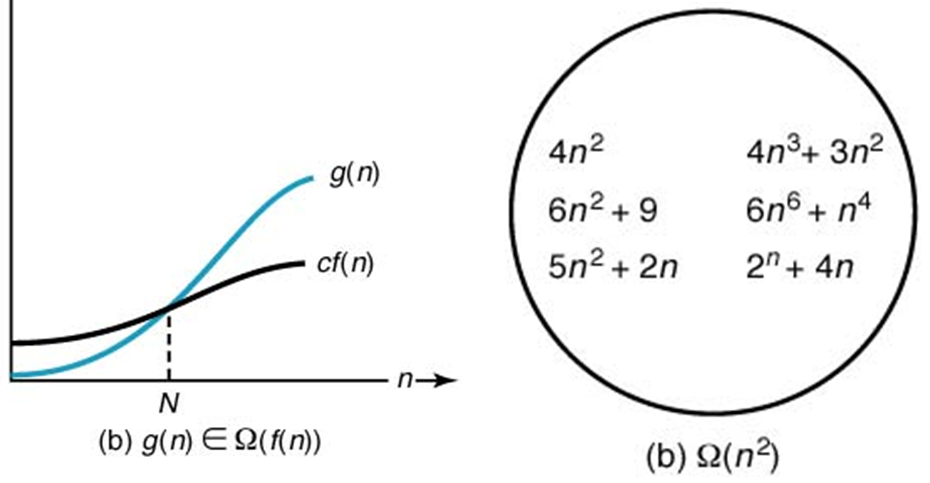
If g(n) ∈ Ω(f(n)), we say that g(n) is omega of f(n)
어떤 함수 g(n)이 $\Omega(n^2)$에 속한다는 말은, 그 함수는 궁극에 가서는 (어떤 임의의 N값보다 큰 값에 대해서는) 어떤 2차 함수 $c \times n^2$의 값보다는 큰 값을 가지게 된다는 것을 뜻한다. 따라서 함수 g(n)은 어떤 2차 함수 $c \times n^2$보다는 궁극적으로 나쁘다고 할 수 있다.
g(n) ∈ Ω(f(n))
- g(n): 분석된 결과
- Ω(f(n)): 적어도 f(n)의 비율로 증가하는 함수. O(f(n))과 대칭적
- g는 f보다 느리게 증가하지 않는다.
an asymptotic lower bound: 점근적 하한
omega는 x가 증가할수록 g(x)보다 항상 스케일이 작은 f(x)를 찾는 것이다.
어떤 알고리즘의 시간복잡도가 Ω(f(n))이라면, 입력의 크기 n에 대해서 이 알고리즘의 수행시간은 아무리 빨라도 f(n)밖에 되지 않는다. 다시 말하면 이 알고리즘의 수행시간은 f(n)보다 절대로 더 빠를 수는 없다는 말이다. (f(n)이 하한)
Theta
For a given complexity function f(n), Θ(f(n)) = O(f(n)) ∩ Ω(f(n)). This means that is the set of complexity functions g(n) for which there exists some positive real constants c and d and some nonnegative integer N such that, for all n ≥ N, c $\times$ f(n) ≤ g(n) ≤ d $\times$ f(n).
Θ(f(n))은 다음을 만족하는 복잡도 함수 g(n)의 집합이다. n ≥ N인 모든 정수 n에 대해서 c $\times$ f(n) ≤ g(n) ≤ d $\times$ f(n)이 성립하는 실수 c > 0와 d > 0, 그리고 음이 아닌 정수 N이 존재한다.
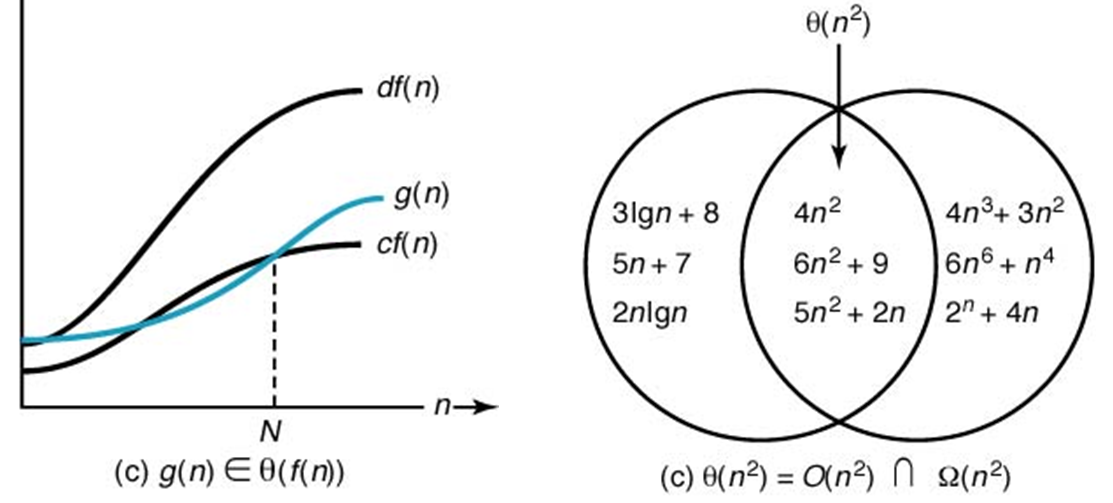
If g(n) ∈ Θ(f(n)), we say that g(n) is order of f(n)
g(n) ∈ Θ(f(n))
- Θ(f(n)) = O(f(n)) ∩ Ω(f(n))
- g(n) : 분석된 결과
- Θ(f(n)) : f(n)의 비율로 증가하는 함수
- g는 f와 같은 정도로 증가한다.
an asymptotic tight bound (O ∩ Ω)
big O는 상한을, omega는 반대로 하한을 찾는 것이므로 실제 수행시간과는 괴리가 있을 수 있다.
$$
\begin{align}
(5n + 7) &\in O(n^2) \\
(6n^6 + n^4) &\in Ω(n^2)
\end{align}
$$
Theta는 big O와 omega의 교집합으로 시간복잡도를 분석하는데 있어 가장 정확한 표기법이다.
Complexity Categories
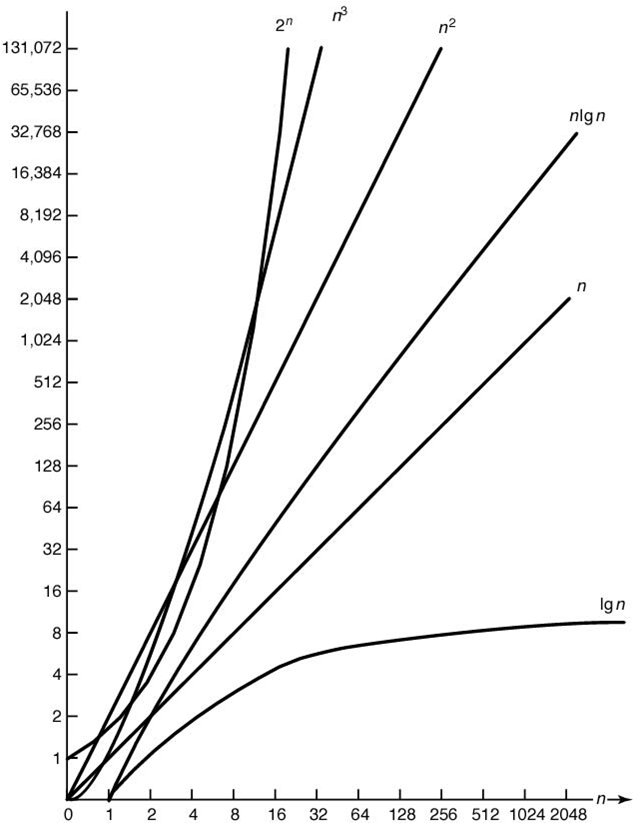
Θ(1): constant time
- 입력크기에 상관없이 수행횟수가 일정하다.
Θ(logn): logarithmic time
Θ(n): linear time
- 수행시간이 입력 크기에 따라 선형적으로 증가함을 의미한다.